投資と複利~株式投資での配当再投資のすすめ
投資と聞くだけで気持ちが後ずさりするのに、さらに複利と聞くと気が滅入ってしまうのはよくわかります。
普段、複利と聞いて真っ先に思い浮かぶのが住宅ローンの金利計算です。
そうです!一般的に複利は借金という言葉とセットでネガティブなイメージを纏っています。
でも、投資の世界では、めっちゃポジティブです。そのあたりをくわしく掘り下げながら説明します。
複利は利子に利子をつけること
仮に100万円の借金をしたとします。
金利はわかりやすく年10%とします。
1年経過すると、借金は110万円になります。
さらに1年返済せず、放置したとします。
ここで、1年前の110万円に対して10%の金利がかかります。
110万円×10%=11万円が利子です。
借金の合計は、110万円+11万円=121万円になります。
この利子に利子がかかる仕組みのことを複利と呼びます。
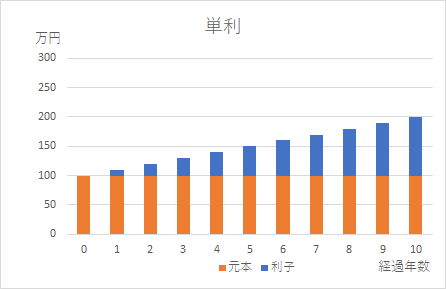
単利は元本を維持、複利は元本に利子を加え続ける
最初に借りたのが、100万円だから…
2年目も元本の100万円に対して10%の10万円でいいですよ….
という場合の合計は、100万円+10万円+10万円=120万円です。
これを単利と呼びます。
でも、このような優しい人はいません。
基本的には、借金は複利で計算されます。
ほとんどの住宅ローンも複利で計算しています。
複利は、100万円の利子10万円が元本に加えられると考えると理解しやすいです。
2年目の元本は利子によって膨れて、(元本が)110万円になったと考えれば良いです。
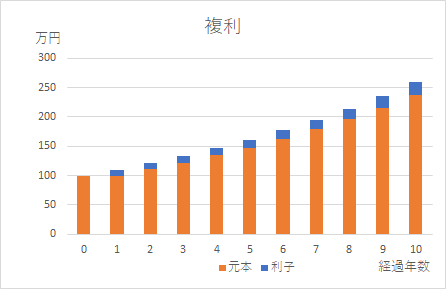
簡単に複利計算する方法は
3年目は121万円に10%の利子が付きますので12万1千円増えて、133万1千円になります。
計算式にすると3年目は、100万円×1.10×1.10×1.10(3回掛けている)=131万1千円となります。
10年目は、 100万円×1.10×1.10×….×1.10(10回掛ける)
= 100万円×1.10^10 = 259万3742円
「^」は、べき乗と呼び、「1.1^10」は、「![]() 」のことです。
」のことです。
そして、利子10%で10年放置すると複利の場合は借金が2.6倍まで膨れ上がることに注目してください。
単利ならば、10万円×10年=100万円という単純な式になり、借金合計は200万円ですね。
もし、利子が3%で10年で計算するなら、100万円×1.03^10=134万3916円となります。
スプレッドシート(エクセル)で計算するなら、シートのセルに「=1000000*1.03^10」と入力すれば計算結果が得られます。
株式投資の値上がりは複利運用の代表
ここでは100万円を株式に投資したとします。
1年後、10%値上がりし110万円になったとします。
金額にすると、100万円×10%=10万円の儲けとなります。
次の年、またもや10%上昇しました。
金額にすると 110万円×10%=11万円の儲けです。
このときの株価は、110万円+11万円ですから、121万円になってます。
株式の上昇も複利での計算になってますね。
株などの価格上昇と借金の利子は別物と考えがちですが、率で計算するものはすべて利子であると捉えて計算することが出来ます。
これからは、率と聞いたら単利なのか、複利なのか、気にしてください。
そして、株式投資の値上がりは複利になります。
複利をグラフで表現する
100万円の投資を行った後、毎年10万円上昇した場合の(単利の)グラフは、以下のようになります。
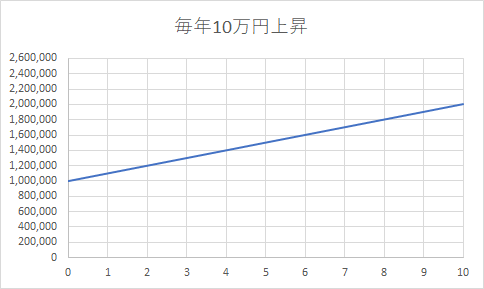
元本の100万円に対して単利で10%ずつ上昇していくイメージです。
この場合、9年目から10年目の上昇率は、200万円÷190万円=1.052…ということで5.2%程度の上昇にとどまっています。
一方、100万円の投資を行った後、毎年10%上昇した場合の(複利の)グラフは、以下のようになります。
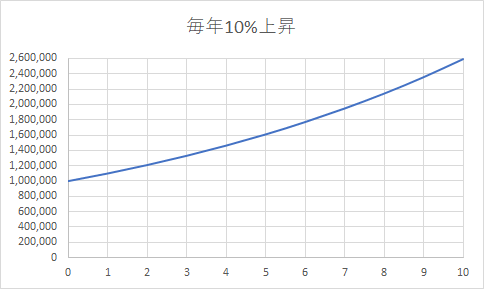
これが借金だったらイヤになりますが、株価だったらホクホクですね。
複利には対数軸が合う
時々、株価のグラフの縦軸が「対数軸」になっているのを見かけたことがあると思います。
対数軸とは、通常1,2,3とひとつずつ増えていく縦軸が、1,10,100といった感じで桁の0が増えていく軸のことです。
上のグラフの縦軸を対数軸にしてみます。
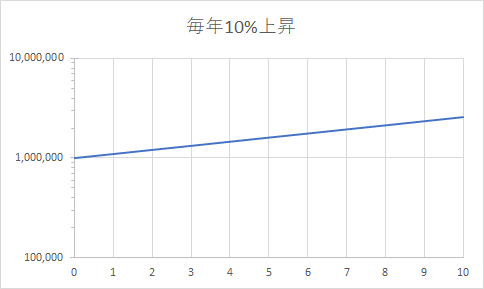
傾きが緩やかになりましたが、グラフの線が直線になったことに注目してください。
直線になっていると言うことは、一定の(複利の)利率で上昇していることを表します。
(複利で上昇する)株式が一定の率で上昇しているかを表すには、対数軸が合うのです。
S&P500のチャートを見て複利を感じる
縦軸が1,2,3と上がる目盛りのことを「線形目盛」と呼びます。すぐ忘れてもらって結構です。
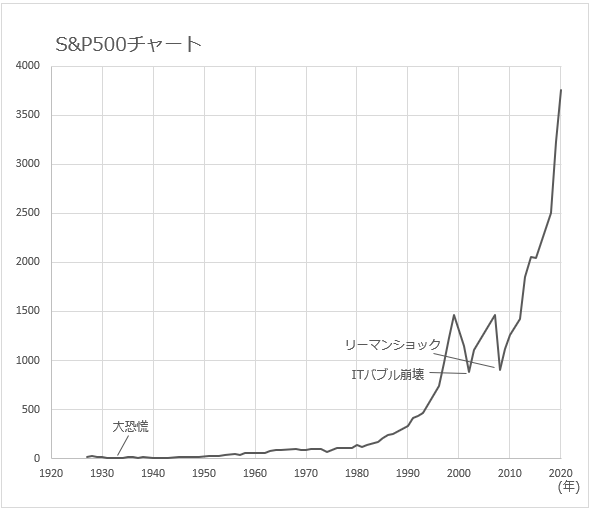
大恐慌が一体どこなのかわからなくなってます。
縦軸を「対数目盛」にします。
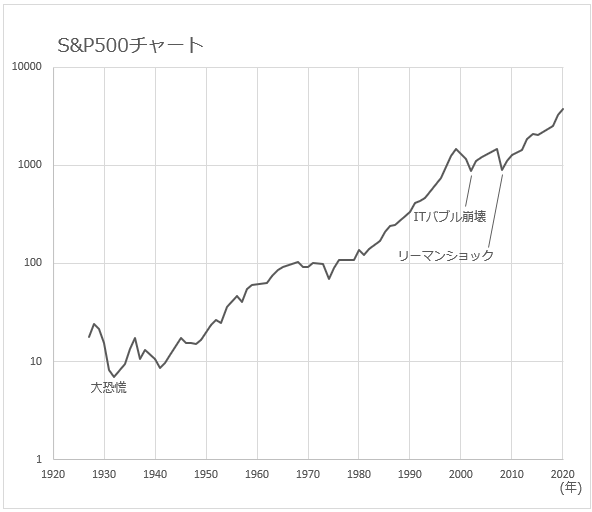
きれいに?右肩上がりの直線ですね。
ITバブル崩壊とリーマンショックで約15年間停滞しましたが、大恐慌の方が下落率も停滞期間も大きいです。
また、ITバブル崩壊前の1995年から1999年までは、上昇ペースが早かったことも読み取れます。
他にもいろいろ言いたいことがありますが、趣旨から外れるので割愛します。
株式投資の配当再投資は複利に複利を加える最強の投資法
株式自体が複利で上昇を続ける点について説明しましたが、株式にはさらに配当というものがあります。
米国では、年に4回支払われることが常です。
年間で株価に対し2%程度(1回あたり0.5%)支払われます。
高配当株は7%なものがあります…ここでは割愛します。
通常配当は現金などで投資した人に支払われます。
ここで申し上げたいことは、この配当で新たな株式を購入するとどうなるのでしょうか。
先のS&P500のチャートに年2%で買増しを想定したグラフを重ねてみます。
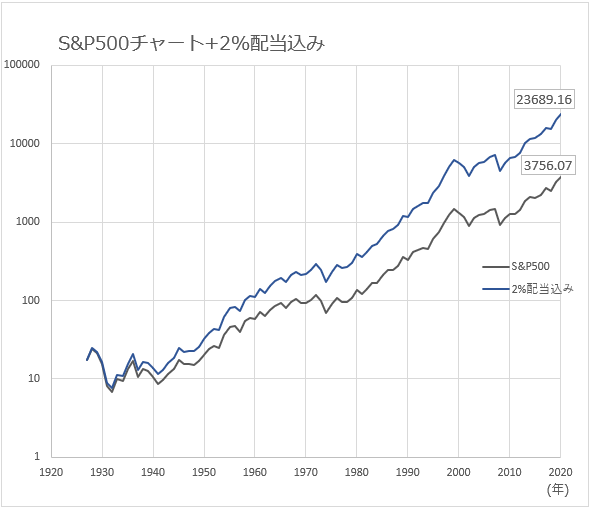
2020年末のS&P500指数の値は3756.07です。
1927年から毎年2%の配当を再投資した場合の2020年末の結果は23689.16です。
93年という長期投資の計算ですので実現性はありませんが、その差は6.3倍です。
この計算、そんなに難しくありません。
毎年2%複利で93年間なので、1.02^93=6.3069倍です。
複利に複利を重ね合わせた効果を実感できたでしょうか。
配当があるのは株式だけです。債券やFX、仮想通貨にはありません。
複利を逆算する計算方法
S&P500は、1927年末から2020年末までの93年間で平均何%で上昇したか?
1927年末の値は17.66で、2020年末の値は3756.07でした。
複利で借金の支払い総額を計算する方法は、
[総額]=[元本] ×(1+[利率])^[年数]なので、
この逆を行えば、複利の平均利率が計算できます。
(1+[利率])=([総額]÷[元本])^(1÷[年数])
です。
早速、計算式に代入してみましょう。
(3756.07÷17.66)^(1÷93) =1.059326
およそ5.9%上昇となりました。
算術平均と幾何平均の違い
複利ではなく、単利で計算するならば、
{(3756.07-17.66)÷ 17.66} ÷ 93 = 2.276倍(227.6%)
つまり、毎年、(17.66×2.276倍=)40.19づつ増えていくと93年後に3756.07になるということです。
これを「算術平均」とよび、単利の計算に用いられます。
代表例が単利の定期預金です。
100万円を預金し1%の金利が付いたとします。
毎年1万円が、定期預金口座ではなく普通預金口座に振り込まれます。
そして次の年も、元本100万円の1%の1万円が普通預金口座に振り込まれます。
複利の定期預金もありますから利用するときは確認しましょう。
ちなみに複利の平均を「幾何平均」と呼びます。
投資信託は自動で配当の再投資を行ってくれる
株式(ETF,ETNを含む)の配当は、主に現金で支払われます。
現金で支払われるときに税金20%が差し引かれるので、再投資しても少し目減りします。
一方、インデックスに連動する投資信託では、株式の配当を内部で再投資してくれます。
この場合は、税金20%がかかりませんので効率よく資産を増やすことが出来ます。
再投資の効果を比較する
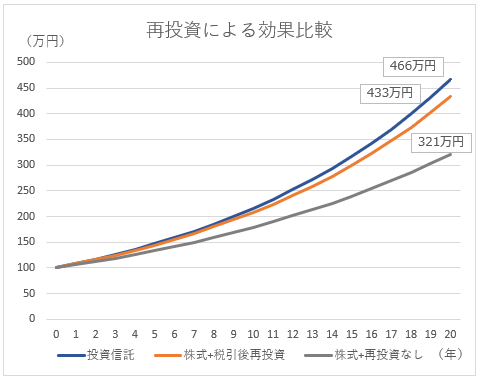
毎年6%で株価上昇、2%の配当がある銘柄を、「投資信託」、「株式+税引後再投資」、「株式+再投資なし」で運用した場合の比較をしました。
100万円を投資し、20年後を比較しました。
「株式+再投資」は、配当利益に対し20%の税を引いたのち再投資する形です。
結果、税金がかかるか否かというよりも、再投資しないと利益がかなり低下することがわかりました。
投資信託の配当は本当に反映されているか
eMAXIS Slim S&P500投資信託の目論見書を読んでみると、「(配当込み)の値動きに連動する投資成果をめざします」と書いてあります。

信じていないわけではありませんが、調べてみます。
年率1.172%反映されていました
2018/7/3時点の値、(eMAXIS Slim S&P500基準価格10038、為替110.59円/ドル、S&P500指数 2713.22)を基準に eMAXIS Slim S&P500の基準価格をS&P500指数に換算して表示しました。
結果は、S&P500指数に概ね追従しつつ、2020/12/30時点で(基準価格がS&P500指数に対して)1.0316倍でした。
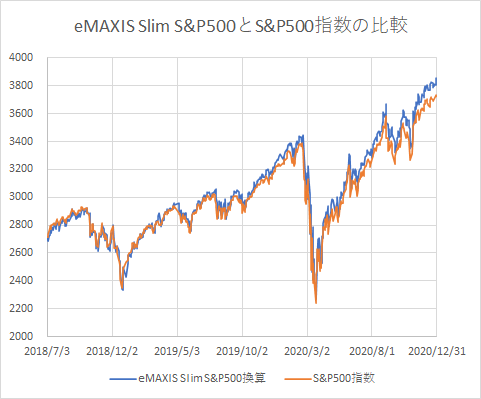
この間、2.67年経過していますので、利率の幾何平均を計算すると、
1.0316^(1/2.67)= 1.01172
S&P500指数に対して、年率1.172%上昇していました。
S&P500に含まれる500社の平均配当率は1~2%と言われていますので妥当かと思っています。
NISAでは、株を買うべきか、投資信託を買うべきか
個人的な意見ですが、
投資効率で言えば、投資信託。
毎年、配当を無税で受け取ってご褒美につかうなら、株式。
長期投資でかつ、投資信託自体に再配当の機能が組み込まれているならば、無理にNISAでなくても良いのではないかと思っています。
つみたてNISAでしたら、株式は買えず、投資信託一択となりますので、迷うことは無くなります。
あとがき
今回の記事では、株式は「なぜ複利で上昇を続けるのか」という本質についての説明を省略しています。
簡単に説明するならば、「会社を経営する者は、持っているリソース(株価×株発行数)を最大限に生かしてリターンを最大にすることを使命とする」に尽きます。
説明しはじめると、どんどん趣旨から外れていくので割愛しました。